Chapter 6
Application of the Atmospheric Model to Projectiles Part A
Escape into Space
A reference, hyperphysics, gives escape
velocity for the earth, in the absence of atmospheric resistance, as 11.2 km/s. This value
is derived by equating the potential energy of an object to its kinetic energy.
Suppose that we found the velocity required at sea level to reach a velocity of
11.2 km per second at a 1000 km above sea level, in the presence of atmosphere.
We might consider that velocity
as a realistic value for escape velocity.
Using the web-based 2D Calculator, (linked at the end of this chapter or available
on the upper row of navigation tabs), an
initial velocity was found meeting the requirement, seen next:
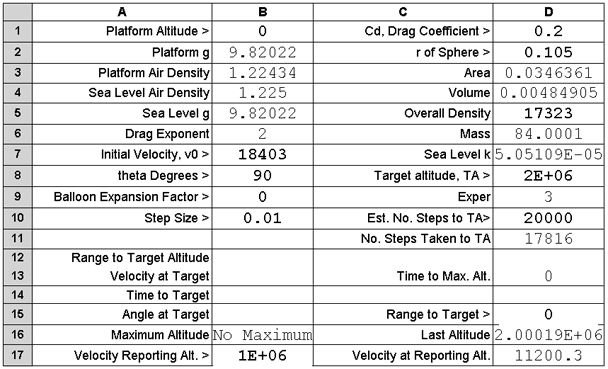
One should note that the velocity objective was marginally exceeded and the object
was still traveling upward when the target altitude was passed.
Could the required initial velocity be reduced? One way to do this is to increase
the length of the shell, and its sea level weight. This is effected in our model
by increasing the density of the object. The effect of doubling the density is shown
next.
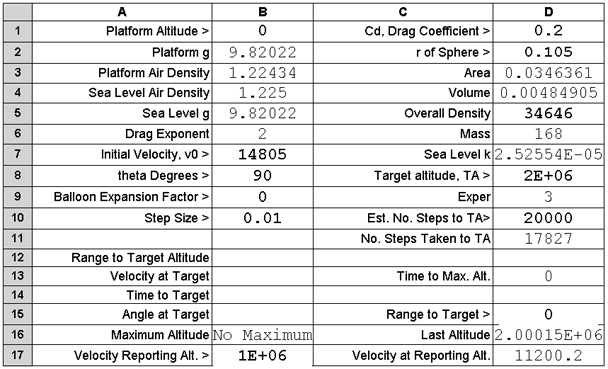
The required initial velocity was reduced by ~ 3600 metres per second.
The greater explosive charge needed to reach escape velocity and corresponding heating make
it quite challenging to use a gun to launch an object into space from the earth.
A long barrel length is required to obtain high muzzle velocity for a shell from the
charge.
Gerald Bull, HARP, and the Babylon Gun
Gerald Bull, see
Space Guns, was born in Canada in 1928.
He received a PhD from the University of Toronto at the age of 23.
He went on to employ a gun to launch weather-sounding probes into the upper atmosphere
above the reach of the weather balloon. The program was named the "High Altitude
Research Program", HARP. For an interesting history of the program see Brief History.
At first Bull employed modified 120 and 175 mm guns to reach altitudes of ~72 km
and ~100 km respectively.
His personal agenda was to go beyond weather probes and put payloads into earth orbit.
To create a supergun, two 400 mm naval guns were welded together, providing a total
length of 30 metres, supported with a superstructure, and set in a fixed site on
the island of Barbados. See media photo gallery
for a set of HARP project images. For more see The HARP Project and the Martlet.
In 1966 the supergun launched a Martlet 2
to an altitude of ~180 km, a record that still stands.
Model the HARP Martlet 2 Launch
This launch was made with a not quite 90-degree elevation so that the payload would
fall harmlessly into the Atlantic. Splash down was within 80 km of the launch site.
The flight time was over 400 seconds.
The Martlet 2 was dart shaped, 13 mm in diameter, and varied in length from 1.27
to 1.68 metres. It was fitted with fins and beveled to induce spin. It weighed about
84 kg. A tight fitting "pusher plate" was employed in the gun barrel to launch it.
Four "petal" arms were used to ensure that it was maintained in an upright position
during launch. These and the pusher fell away within a few km of the launch
site.
It is believed that radar was used to track the altitude. How accurately?
What was the length of the Martlet that was used for the launch? Should one presume
that it was the shorter version that weighed 84 kg and that the longer version weighed
proportionately more, 110 kg?
Atmospheric density depends on temperatures and varies with season, latitude and
gravity.
There is a bulge in the shape of the Earth near the equator, which makes the equator
about 21 km more distant from the gravitational centre of the Earth than polar positions.
The "Earth" employed in our model is spherical. It would be possible to model
at a greater distance from the Earth centre to take into account some bulge at
the launch site.
Given all the unknowns, we are content to
make some choices and then vary them some to obtain results similar to the reported
results. Greatest reliance is placed on flight time.
The web version of the spreadsheet 2D Calculator is used to model the flight of this dart. Case 4
is chosen. See the results next.
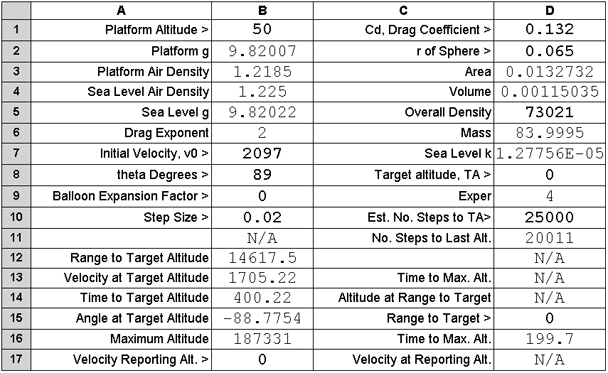
The guessed Platform Altitude was 50 meters and Target Altitude 0.0 metres, for splash down at sea level. An initial velocity of 2097 metres per second
was chosen as
"nearly 2100 metres per second". A density of 73021 was chosen so that
the sea level
weight of the dart would be 84 kg, corresponding to the shortest Martlet
2. The elevation was chosen as 89 degrees. The drag was then adjusted to bring the flight
time to just over 400 seconds.
Splashdown occurred at ~ 14.6 km from the launch site.
Although nothing
is known to the writer about the drag values achieved by the Martlet 2 darts, the found value of 0.132 does not seem untoward.
The result provides a maximum altitude of ~ 187 km, higher than the reported value
of 180 km.
All things considered, the writer is pleased at getting in the ballpark of
the reported altitude record.
Web Version of the Excel Calculator
The web version of the 2D Excel calculator will be further described in the next
topic of this chapter. With it the viewer will be in a position to experiment
with different assumptions than those employed by this writer.
The Babylon Gun
The "Space Guns" reference goes on to tell of Gerald Bull's
continuing determination to build a super gun for space launches. He sold the idea
to Saddam Hussein. The
Iraqis were interested and provided funds.
The gun was to have a 1 metre bore, a length of 156 metres and be capable of putting
a 200 kg payload into orbit.
Parts for the gun were received but it was never assembled.
Gerald
Bull was killed, shot, in Paris in March 1990.
In 1991, United Nations inspectors discovered sections of the super gun and these were
destroyed.
Next:
The next topic includes:
1. Ballistics of a model of a grenade launcher.
2. More description of the web based version of the 2 D spreadsheet calculator that includes:
a close approximation to the 1976
U.S. Standard Atmosphere, the effect of atmosphere buoyancy and the Raleigh approximation
for atmospheric resistance that is proportional to the square of velocity.